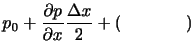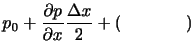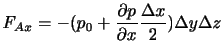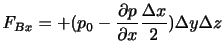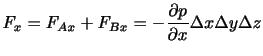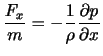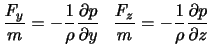: 応力と応力テンソル
: 流体にはたらく基本的な力
: 万有引力
目次
体系の順番としては次に応力を導入するのが筋かもしれないが,やや難しいテンソルの表記に触れる前に気圧傾度力の物理的なイメージを捕らえておくことにする.気圧傾度力を考えるにあたって,図2.2のような
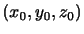 を中心とする微小体積(
を中心とする微小体積(
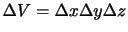 )の空気塊を考える.周囲の空気は体積要素の壁に運動量を連続的に分け与える.この単位面積,単位時間あたりの運動量の輸送が,周囲の空気によって体積要素の壁に及ぼされる圧力にすぎない.体積要素の中心における圧力を
)の空気塊を考える.周囲の空気は体積要素の壁に運動量を連続的に分け与える.この単位面積,単位時間あたりの運動量の輸送が,周囲の空気によって体積要素の壁に及ぼされる圧力にすぎない.体積要素の中心における圧力を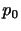 とすると,図1.2の壁Aの圧力はテイラー展開を用いて,
と表される.高次の項を無視すれば,壁Aにおいて体積要素にはたらく気圧力は,
とすると,図1.2の壁Aの圧力はテイラー展開を用いて,
と表される.高次の項を無視すれば,壁Aにおいて体積要素にはたらく気圧力は,
図 2.2:
流体要素にはたらく気圧傾度力の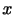 方向成分
方向成分
l6.5cm
|
である.ここで,
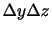 は壁Aの面積である.同様にすれば,壁Bにおいて体積要素にはたらく気圧力は
となる.よって,体積要素にはたらく正味の気圧力の
は壁Aの面積である.同様にすれば,壁Bにおいて体積要素にはたらく気圧力は
となる.よって,体積要素にはたらく正味の気圧力の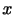 成分は,
である.正味の圧力はその力の方向の圧力微分に比例するので,この力は気圧傾度力(pressure gradient force)と呼ばれる.微小体積の質量
成分は,
である.正味の圧力はその力の方向の圧力微分に比例するので,この力は気圧傾度力(pressure gradient force)と呼ばれる.微小体積の質量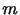 は密度
は密度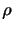 とその体積の積であるので,
とその体積の積であるので,
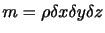 である.よって,単位質量あたりの圧力傾度力の
である.よって,単位質量あたりの圧力傾度力の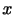 成分は,
となる.同様にすれば,単位質量あたりの圧力傾度力の
成分は,
となる.同様にすれば,単位質量あたりの圧力傾度力の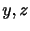 成分はそれぞれ,
となるので,単位質量あたりの全方向の圧力傾度力はベクトル表記を使えば,
成分はそれぞれ,
となるので,単位質量あたりの全方向の圧力傾度力はベクトル表記を使えば,
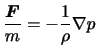 |
(3.4) |
と表される.圧力傾度力は,圧力自身でなく圧力場の勾配に比例するという点に注意されたい.
Yuta
平成22年1月23日