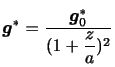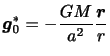: 気圧傾度力
: 流体にはたらく基本的な力
: 流体にはたらく基本的な力
目次
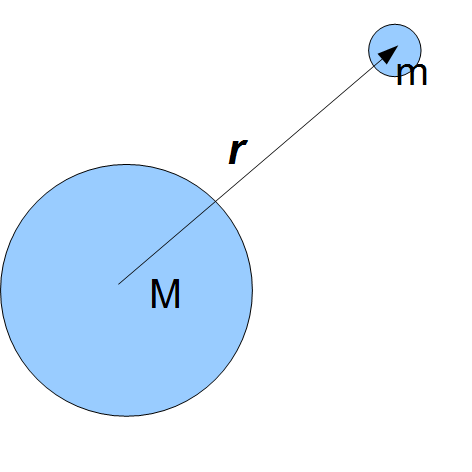
図1.1のように2つの物体があるとき,その間には物体の質量に比例し,2物体間の距離の2乗に反比例する引力が働く.この力を万有引力(universal gravitation)という.
図 2.1:
球形をした2物体の間に働く引力
l6.5cm
|
2つの物体の質量をそれぞれ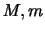 とし2つの物体の位置ベクトルの相対ベクトルを
とし2つの物体の位置ベクトルの相対ベクトルを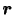 とする(図参照).このとき質量
とする(図参照).このとき質量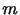 に及ぼす質量
に及ぼす質量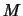 の引力
の引力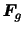 は,
は,
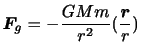 |
(3.2) |
となる。ただし
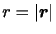 であり,
であり,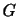 は万有引力定数(
は万有引力定数(
![$ =6.673 \times 10^{-23}{\rm\;[kg^{-1}m^3s^{-2}]}$](img21.gif) )である.
)である.
式(2.2)は,一般的には容積が無限小であるような仮想的なもの(質点)に対して適用されるべきであるが,球対称な質量分布を持つような物体に対しては,その2物体の中心間の距離を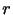 として適用することができる.したがって,地球の質量を
として適用することができる.したがって,地球の質量を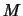 ,大気あるいは海洋の微小部分の質量を
,大気あるいは海洋の微小部分の質量を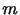 とすれば,単位質量あたりの微小部分におよぼす地球の引力は,
とすれば,単位質量あたりの微小部分におよぼす地球の引力は,
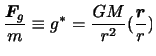 |
(3.3) |
である.平均海面から測った高さを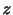 ,地球の平均半径を
,地球の平均半径を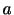 (
(
![$ =6371{\rm\; [km]}$](img26.gif) )とすると,
)とすると,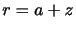 であるので,
である.ここで,
は平均海面における引力である.気象学では
であるので,
である.ここで,
は平均海面における引力である.気象学では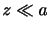 であるので,
であるので,
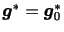 となり,地球の引力は高さによらず一定として取り扱えるものとする.
となり,地球の引力は高さによらず一定として取り扱えるものとする.
Yuta
平成22年1月23日
![]() とし2つの物体の位置ベクトルの相対ベクトルを
とし2つの物体の位置ベクトルの相対ベクトルを![]() とする(図参照).このとき質量
とする(図参照).このとき質量![]() に及ぼす質量
に及ぼす質量![]() の引力
の引力![]() は,
は,
![]() として適用することができる.したがって,地球の質量を
として適用することができる.したがって,地球の質量を![]() ,大気あるいは海洋の微小部分の質量を
,大気あるいは海洋の微小部分の質量を![]() とすれば,単位質量あたりの微小部分におよぼす地球の引力は,
とすれば,単位質量あたりの微小部分におよぼす地球の引力は,