連続体への運動方程式の適用

ニュートンの運動方程式(2.1)は質点の運動を記述する．なので質点として物体を構成する膨大な数の粒子を選び，それぞれの粒子に対して運動方程式を適用することが考えられる．しかし，そのようなことをしなくても剛体の場合は，その重心の運動（自由度3の並進運動）と重心周りの回転（各方向軸に対して自由度3の回転）に注目して，合計6個の自由度に関する方程式で剛体の運動を記述できる．しかし，液体や気体は剛体とは異なり外部的な力を加えられると変形してしまうためそのような方法は使えない．液体や気体のような流体に対して運動方程式を適用するためには，連続体という概念を取り入れる必要がある．

流体内部のある一点の（十分な量の分子を含む）微小体積について物理量の平均値が取れるとすると，その点における物理量はその点の連続関数として捉えることができる．このように，ミクロな分子の物性や運動を微小体積内の平均値で置き換えることによって得られる連続的な物理的性質を持つ仮想的な物体は，連続体（continuum）と呼ばれる．また，このような近似は連続体近似と呼ばれる．流体力学では，流体を連続体として取り扱う．

このような連続体では，密度$\rho$は以下のように定義される．流体が質量$m$を持った粒子（原子や分子）で構成されていする。流体中の点Pを含む微小体積$\delta v$をとり，そこに含まれる粒子の個数を$N$個，点Pの位置ベクトルを$\bm{r}$，点Pにおける密度を $\rho(\bm{r},t)$とすると，

$$\rho(\bm{r},t)\equiv\dfrac{Nm}{\delta v}$$

である．

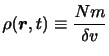
　微小体積内に含まれる分子が少なすぎる場合，分子の衝突が少ないため気体の物理的な性質がうまく平均化されない．このような場合には連続体近似は成り立たなくなる．