静止流体における応力テンソル

さて，上で定義した応力を用いて流体の特徴づける．流体は固体に比べて容易に変形するのが特徴である．しかし，圧縮には抵抗する．そこで流体を，体積変化なしに変形させようとするといかなる作用にも抵抗できないものとして定義する．主軸系で表した応力テンソル（2.16）を平均垂直応力

$$\tau_{m} = \dfrac{1}{3} \tau_{ii}$$

を使って次のよう2つに分割することを考える.

$${\rm\; diag}(\dfrac{1}{3}\tau_{ii}, \dfrac{1}{3}\tau_{ii}, \dfrac{1}{3}\tau_{ii})$$ (3.19)

および

$${\rm\; diag}(\tau^{\prime }_{1} - \dfrac{1}{3}\tau_{ii}, \tau^... ...e }_{2} - \dfrac{1}{3}\tau_{ii}, \tau^{\prime }_{3} - \dfrac{1}{3}\tau_{ii})$$ (3.20)

平均垂直応力（2.19）は，どのような向きの面に対しても同じ大きさの法線応力のみがはたらく.（2.19）のようなテンソルは等方テンソルという.この等方的な応力テンソルは，図2.5のような状態が対応する.このような圧縮には流体は抵抗し，静止状態を維持することができる.

図 2.5: 等方的圧縮

図 2.6: 体積変化なしに変形しようとする応力状態

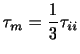
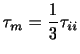
一方，（2.20）は等方的な応力テンソルからのずれ（偏差テンソル）であり，そのトレースは （2.17）から0となることが分かる.したがって，対角成分の少なくとも１つは正，１つは負であって，図2.6のような体積変化なしに純粋に流体要素を変形しようとする応力状態である.流体はこれに抵抗できない.体積力は高次の無限小なので，体積力でこの変形に対抗することもできない.したがって，このような応力状態が存在すると流体は静止状態を保つことができない.故に，流体が静止しているときには，

$$\tau^{\prime}_{1} = \tau^{\prime}_{2} = \tau^{\prime}_{3} = \dfrac{1}{3} \tau_{ii}$$ (3.21)

を満たさなければならない.結局，静止流体に対しては応力テンソルは，

$$\tau_{ij} = -p \delta_{ij}$$ (3.22)

と書ける. $p(= - \tau_{ii}/3)$は$\bm{r}$のみの関数であり，圧力（pressure）と呼ばれる.（2.22）のように右辺に負号をつけるのは，圧力状態で$p$が正になるようにするためである.（2.22）は，法線$\bm{n}$を持つ面要素を通じて作用する単位面積当たりの力が$-p\bm{n}$であることを意味する.また，この静止流体の圧力$p$は，熱力学的な圧力$p_{e}$そのものである.

いま，静止状態，運動状態にかかわらず，接線応力が常に0であると仮定する.このとき法線応力は面の選び方によらず一定である.つまり，この場合にも応力テンソルは（2.22）の形となる.なぜなら，（2.18）が任意の法線ベクトル $\bm{n}^{\prime}$に対して， $\bm{n}^{\prime}$と平行であるためには（2.21）が成立しなければならないからである.

運動状態にある流体は，一般に粘性（内部摩擦力）によって接線応力を生じる.このように粘性によって接線応力を生じるような流体を粘性流体（viscous fluid）という.一方，運動状態でも接線応力を生じない仮想的な流体を考え，これを非粘性流体（inviscid fluid）または完全流体（perfect fluid）と呼ぶ.完全流体では運動中でも応力テンソルは静止状態と同じ（2.22）の形となる.つまり，完全流体の場合も応力として等方的な圧力のみがはたらく.しかし，一般に流体が運動しているときの圧力$p$の値は静止しているときの値とは異なる.ふつう，完全流体では局所熱平衡が成り立つと仮定するので，（2.22）の圧力 $p(\bm{r},t)$は局所的な熱力学的圧力 $p_{e}(\bm{r},t)$に等しい.

流体の粘性を無視して完全流体のような仮想的な流体を考えるのは，それにより数学的な取り扱いが粘性流体に比べてはるかにシンプルになるからである.さらに，完全流体が現実の流体のふるまいをよい近似で与える場合がしばしばあるからである.