



: 静止流体における応力テンソル
: 応力と応力テンソル
: 応力と応力テンソル
目次
まず応力について考える.一般に応力はそれが作用する面の向きに依存する.図2.3のように時刻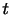 において,流体中の点
において,流体中の点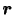 で単位法線ベクトル
で単位法線ベクトル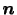 と面積
と面積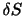 を持つ面を考える.この面を通じて面の表側(
を持つ面を考える.この面を通じて面の表側(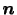 が向いている側を表とする)の流体が裏側の流体に及ぼす力を,
が向いている側を表とする)の流体が裏側の流体に及ぼす力を,
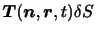 |
(3.5) |
と書き,単位面積当たりの力
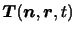 を時刻
を時刻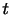 ,点
,点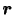 においてその面に作用する応力(stress)という.
においてその面に作用する応力(stress)という.
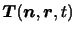 の
の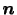 方向成分は法線応力(normal stress),接平面に平行な成分は接線応力(tangential stress)と呼ばれる.また面の裏側の流体が表側の流体に及ぼす応力は,
方向成分は法線応力(normal stress),接平面に平行な成分は接線応力(tangential stress)と呼ばれる.また面の裏側の流体が表側の流体に及ぼす応力は,
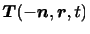 と表される.したがって,作用反作用の法則より,
と表される.したがって,作用反作用の法則より,
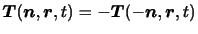 |
(3.6) |
が成り立つ.ゆえに,法線応力が正ならばその面を通じて流体は引っ張り合い,負ならば押し合っていることになる.以後,
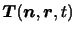 の
の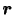 ,
,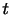 を省略する.
を省略する.
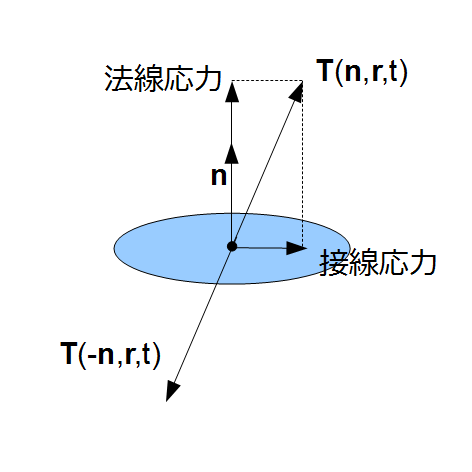
図 2.3:
面の向きと応力
|
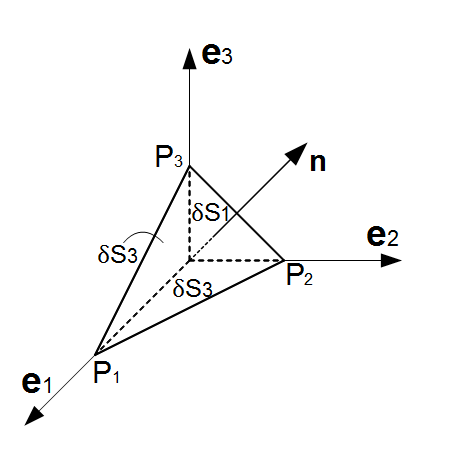
図 2.4:
座標軸に垂直な3つの面を持つ微小な四面体
|
次に,図2.4の微小な四面体にはたらく力のつり合いを考える.この四面体にはたらく力は,慣性力,外力,4つの面を通じて作用する面積力である.慣性力と外力は体積力であり,四面体の長さのスケールを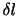 とすると,
とすると,
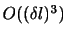 である.これに対して面積力は
である.これに対して面積力は
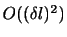 であるから,
であるから,
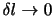 のときには体積力の寄与が無視できて,四面体の4つの面に作用する面積力のつり合いの式として,
のときには体積力の寄与が無視できて,四面体の4つの面に作用する面積力のつり合いの式として,
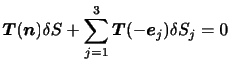 |
(3.7) |
を得る.ここで,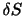 は
は
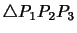 の面積,
の面積,
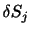 は
は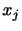 軸に垂直な面の面積である.また,
軸に垂直な面の面積である.また,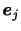 は
は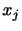 軸方向の単位ベクトルである.ベクトル
軸方向の単位ベクトルである.ベクトル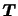 の
の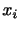 成分を
成分を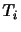 と表す.すなわち,
と書け,
と表す.すなわち,
と書け,
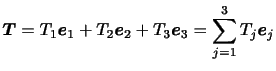 |
(3.8) |
ということである.さらに,(2.8)にアインシュタインの縮約記法を用いれば,
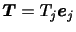 |
(3.9) |
と表される.同様の記法を(2.7)に使えば,次のように書ける.
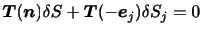 |
(3.10) |
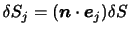 であることと,及び(2.6)を用いれば,(2.7)より,
であることと,及び(2.6)を用いれば,(2.7)より,
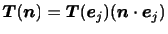 |
(3.11) |
を得る.したがって,3つの座標軸に垂直な面に作用する応力
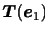 ,
,
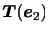 ,
,
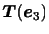 がわかれば任意の面に作用する応力
がわかれば任意の面に作用する応力
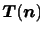 を知ることができる.
を知ることができる.
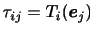 |
(3.12) |
と定義すれば,
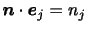 なので,(2.11)は,
なので,(2.11)は,
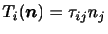 |
(3.13) |
と書ける.この9個の量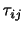 を成分とする量を応力テンソル(stress tensor)という.応力テンソルの特徴は以下のようになる.
を成分とする量を応力テンソル(stress tensor)という.応力テンソルの特徴は以下のようになる.
- テンソルの定義により
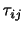 は,
は,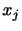 軸に垂直な面の
軸に垂直な面の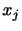 の大きい方の側が小さい方の側に作用する単位面積当たりの力
の大きい方の側が小さい方の側に作用する単位面積当たりの力
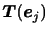 の
の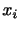 軸方向の成分である.
軸方向の成分である.
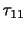 ,
,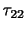 ,
,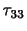 が法線応力,
が法線応力,
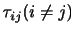 が接線応力である.
が接線応力である.
- 応力テンソルは,
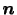 に無関係であり,
に無関係であり,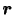 と
と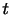 のみによって決まる.そして,2階テンソル
のみによって決まる.そして,2階テンソル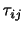 がベクトル
がベクトル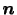 をベクトル
をベクトル
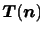 に対応させる線形作用素の役割をしている.
に対応させる線形作用素の役割をしている.
- 応力テンソルは対称テンソルである.(付録A1,A2参照)
いま,ある法線ベクトル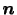 を持つ面に作用する応力が,
を持つ面に作用する応力が,
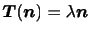 |
(3.14) |
を満たすとする.このとき,その面には大きさ
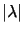 の法線応力しか作用しない.(2.12)を用れば,(2.14)は,
の法線応力しか作用しない.(2.12)を用れば,(2.14)は,
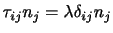 |
(3.15) |
となる.ここで
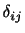 はクロネッカーのデルタ(Kronecker delta)であり,
はクロネッカーのデルタ(Kronecker delta)であり,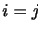 のとき0で
のとき0で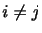 のとき1である.(2.15)は対称行列
のとき1である.(2.15)は対称行列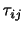 の固有値問題であり,対称行列の性質から重複度も数えれば3個の実固有値
の固有値問題であり,対称行列の性質から重複度も数えれば3個の実固有値
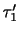 ,
,
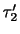 ,
,
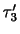 が存在する.また,その互いに異なる固有値に対応する固有ベクトル
が存在する.また,その互いに異なる固有値に対応する固有ベクトル
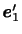 ,
,
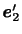 ,
,
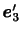 は3次元ベクトル空間の直交基底となる.よって,これらの固有ベクトルを新しい直角座標系
は3次元ベクトル空間の直交基底となる.よって,これらの固有ベクトルを新しい直角座標系
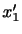 ,
,
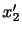 ,
,
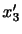 の基底に選べば,座標軸に垂直な面にはそれぞれ法線応力
の基底に選べば,座標軸に垂直な面にはそれぞれ法線応力
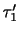 ,
,
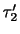 ,
,
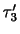 のみが作用するので,新しい系での応力テンソルの表示行列は,
のみが作用するので,新しい系での応力テンソルの表示行列は,
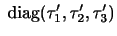 |
(3.16) |
となる.ここで,diag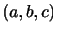 は
は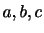 を対角成分とする対角行列を意味する.この
を対角成分とする対角行列を意味する.この
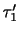 ,
,
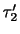 ,
,
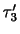 を主応力(principal stress)といい,また対応する新しい座標軸を応力テンソルの主軸(principal axes of stress tensor)という.
を主応力(principal stress)といい,また対応する新しい座標軸を応力テンソルの主軸(principal axes of stress tensor)という.
固有値はスカラー量なので回転に対しても不変である.よって,固有多項式も回転に対して不変であるはずであり,固有方程式の2次の項の係数に対応する行列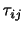 のトレースも直角座標系の回転に対して不変である.すなわち,
のトレースも直角座標系の回転に対して不変である.すなわち,
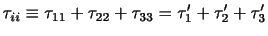 |
(3.17) |
が成り立つ.また,主軸系においては,法線
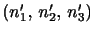 を持つ面要素を通して作用する応力は,
を持つ面要素を通して作用する応力は,
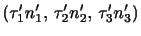 |
(3.18) |
となる.




: 静止流体における応力テンソル
: 応力と応力テンソル
: 応力と応力テンソル
目次
Yuta
平成22年1月23日
![]() を持つ面に作用する応力が,
を持つ面に作用する応力が,
![]() のトレースも直角座標系の回転に対して不変である.すなわち,
のトレースも直角座標系の回転に対して不変である.すなわち,