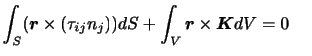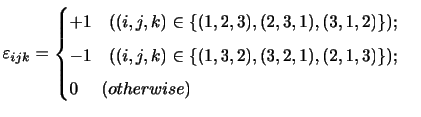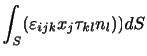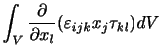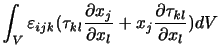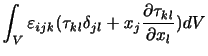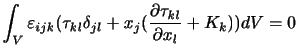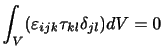: 参考文献
: 応力に関する補足
: 連続体のつり合い
目次
次に,トルクの合計が0になる条件を導く.連続体のある領域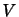 (その表面を
(その表面を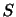 とする)において,領域表面にはたらく応力
とする)において,領域表面にはたらく応力
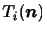 のトルクと,領域にはたらく体積力
のトルクと,領域にはたらく体積力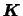 のトルクがつり合うとき,
のトルクがつり合うとき,
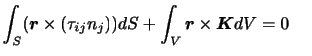 |
(A..47) |
を満たす.なお,直交座標系を使うとして添え字の上下には配慮しないものとする.また,外積はテンソルで表記すれば,
となる.ここで,
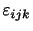 はレヴィ・チヴィタ(Levi-Civita)の記号であり,
と定義される.これを用いれば,(付録A.4)は,
はレヴィ・チヴィタ(Levi-Civita)の記号であり,
と定義される.これを用いれば,(付録A.4)は,
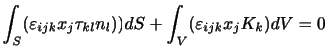 |
(A..48) |
となる.
(付録A.5)の第1項は発散の定理により,
となる.ここで
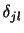 はクロネッカーのデルタ(Kronecker delta)であり,
はクロネッカーのデルタ(Kronecker delta)であり,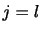 のとき0で
のとき0で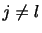 のとき1である.
のとき1である.
よって(付録A.5)は,
となる.また,つり合いの式(付録A.3)より積分内の第2項は0であるので,結局
となる.ここで領域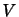 は任意に選ぶことができるので,上式が恒等的に成り立つためには,
を満たさなければならない.したがって,モーメントの合計が
は任意に選ぶことができるので,上式が恒等的に成り立つためには,
を満たさなければならない.したがって,モーメントの合計が であるという物理的な制約は,応力テンソルが対称テンソルであること,すなわち
を要請する.
であるという物理的な制約は,応力テンソルが対称テンソルであること,すなわち
を要請する.
Yuta
平成22年1月23日