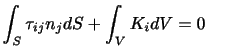連続体のつり合い

まず，力の合計が0になる条件を導く．続体のある領域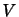$V$（その表面を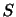$S$とする）において，領域表面にはたらく応力 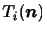$T_i(\bm{n})$と，領域にはたらく体積力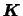$\bm{K}$の合計がつり合うとき，

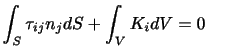$$\int_{S} \tau_{ij}n_j dS + \int_{V} K_{i}dV = 0$$ (A..44)

を満たす．ここで，発散の定理を用いれば（付録A.1）は，

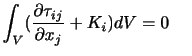$$\int_{V}(\dfrac{\partial \tau_{ij}}{\partial x_{j}} + K_{i})dV = 0$$ (A..45)

となる．いま領域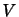$V$は任意なので，（付録A.2）が恒等的に成り立つためには体積積分の中身が０でなければならない．よって，連続体についてのつり合いの式

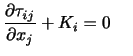$$\dfrac{\partial \tau_{ij}}{\partial x_{j}} + K_{i} = 0$$ (A..46)

を得る．