



: 質量保存則
: 流体運動の記述法
: オイラー的記述
目次
考えている物理量を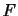 とする.これは,オイラー的記述では
とする.これは,オイラー的記述では
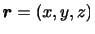 と時間
と時間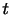 の関数となる.いま注目する流体粒子が時刻
の関数となる.いま注目する流体粒子が時刻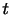 において位置
において位置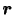 にいたとし,微小時間
にいたとし,微小時間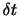 後の時刻
後の時刻
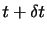 にはその流体粒子は位置
にはその流体粒子は位置
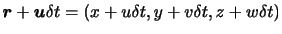 にきているとする.したっがって,その間の
にきているとする.したっがって,その間の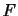 の増分
の増分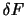 は,
は,
である.よって,特定の流体粒子に注目したときの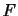 の時間変化の割合は,
となる.また,物理量
の時間変化の割合は,
となる.また,物理量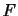 は任意なので微分演算子として表せば,
は任意なので微分演算子として表せば,
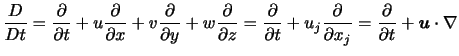 |
(6.39) |
となる.
ここで,流体粒子の加速度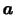 は速度
は速度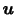 のラグランジュ微分として得られるので,
のラグランジュ微分として得られるので,
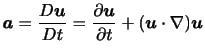 |
(6.40) |
である.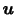 が時間によらない(
が時間によらない(
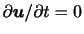 )とき,流れは定常(steady)といわれる.(3.3)から流れが定常であっても,流体粒子が流れていく方向に速度場が変化していれば加速度はゼロでないことに注意が必要である.
)とき,流れは定常(steady)といわれる.(3.3)から流れが定常であっても,流体粒子が流れていく方向に速度場が変化していれば加速度はゼロでないことに注意が必要である.
Yuta
平成22年1月23日
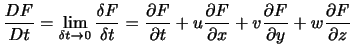
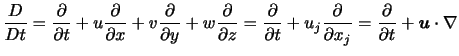
![]() は速度
は速度![]() のラグランジュ微分として得られるので,
のラグランジュ微分として得られるので,