ラグランジュ的記述

ラグランジュ的記述では，流体運動にともなって連続体としての流体を構成する粒子が時間的にどのように動くかに注目する．つまり，注目する微小な体積（control volume）は，目印をつけた無限小の流体粒子の塊を指すことになる．流体粒子の運動とともに注目する微小体積も移動するため，同じ微小体積内は常に同じ流体粒子を含む．目印は，各流体粒子の初期時刻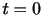$t=0$での位置ベクトル 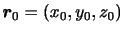$\bm{r}_{0} = (x_0,y_0,z_0)$をとることが多い．ここで，時刻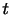$t$での流体粒子の位置ベクトルを 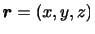$\bm{r}=(x,y,z)$とすれば，

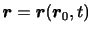$$\bm{r} = \bm{r}(\bm{r}_{0}, t)$$ (6.38)

と表される．ただし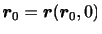， $\bm{r}_0 = \bm{r}(\bm{r}_0, 0)$である．

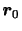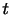この記述において，流体粒子の初期位置$\bm{r}_0$と時間$t$が独立変数であり，粒子の位置ベクトル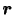$\bm{r}$などが従属変数である．例えば，初期に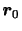$\bm{r}_0$にいた流体粒子に注目してその位置ベクトルの時間変化率を求めれば，その粒子の速度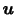$\bm{u}$を求めたことになる．つまり，

$$\bm{u} = \bm{u}(\bm{r}_0, t) = \dfrac{\partial \bm{r}}{\partial t}$$

と書ける．ラグランジュ的記述は，特定の流体要素を使って最も簡単に記述される保存則を導く際に便利である．