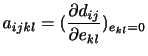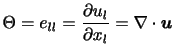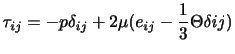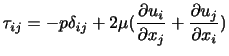: 2
: 運動している流体と応力テンソル
: 流体の局所的運動と変形
目次
静止流体においては前述したように,応力は法線成分しか持たず,法線応力の大きさはそれが作用する向きによらない.つまり,応力テンソルは,
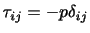 |
(3.29) |
と表されることを示した.また,接線応力が表れないと仮定すれば(完全流体),運動している流体の場合でも,応力テンソルは(2.29)のように表されるのであった.しかし,実際の(相対)運動をしている流体では粘性のために接線応力が現れる.また,一般に面の向きによって接線応力の大きさが異なる.したがって,運動している流体の圧力をあらためて定義する必要がある.ここで,運動している流体の圧力を平均の法線応力に負号をつけた
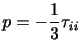 |
(3.30) |
によって定義する.静止流体や完全流体の場合の圧力も上の関係を満たしているので,(2.30)の定義はそれらの拡張となっている.また,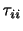 は座標系の回転に対して不変であり,(2.30)の定義はこの点でも好都合である.(2.30)は純粋に力学的な圧力の定義である.
は座標系の回転に対して不変であり,(2.30)の定義はこの点でも好都合である.(2.30)は純粋に力学的な圧力の定義である.
このとき,応力テンソルを等方的な圧力とそれからのずれの2つに分けると便利である.
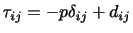 |
(3.31) |
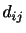 は応力テンソルの非等方的な部分で,接線応力もたらすと同時に対角成分は0である.
は応力テンソルの非等方的な部分で,接線応力もたらすと同時に対角成分は0である.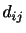 は偏差応力テンソル(deviatoric stress tensor)と呼ばれ,もっぱら流体が相対運動をしていることによって生じる.
は偏差応力テンソル(deviatoric stress tensor)と呼ばれ,もっぱら流体が相対運動をしていることによって生じる.
空気や水のような通常の流体では,図2.10のような剪断流に対して,粘性のために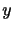 軸に垂直な面を通じて
軸に垂直な面を通じて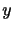 の大きい側が小さい側に
の大きい側が小さい側に
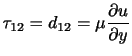 |
(3.32) |
だけの接線応力を及ぼす.このとき,同時に小さい側は大きい側に同じ大きさの逆向きの接線応力を及ぼす.この応力は速度差を減らす方向にはたらく.このように速度勾配に比例する接線応力を生ずるような流体をニュートン流体(Newtonian fluid)と呼ぶ.大気の運動を記述する際には,この「速度勾配に比例する接線応力(=ニュートン流体)」を仮定する.一方,接線応力と速度勾配が比例しない流体を非ニュートン流体と呼ぶ.このニュートン流体の関係は,偏差応力テンソルと速度勾配テンソルが比例関係にあることを示している.流体要素全体が並進運動あるいは剛体運動している場合は相対運動を生じないので,そういった運動は粘性力に関係しない.したがって,速度勾配テンソルの中で変形速度テンソルのみが偏差応力テンソルに関係していると考えられる.そこで,
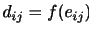 という関係があるとする.さらに,
という関係があるとする.さらに,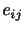 が十分小さいとしてテイラー展開を行い,2次以上の項を無視すれば,
が十分小さいとしてテイラー展開を行い,2次以上の項を無視すれば,
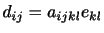 |
(3.33) |
と書ける.ここで,
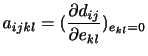 |
(3.34) |
であり,これらは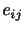 によらない物質定数である.
によらない物質定数である.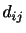 と
と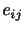 は2階テンソルであるので,
は2階テンソルであるので,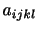 は4階テンソルである.さらに,流体が等方的な物質であれば,これらは等方的なテンソルでなければならない.一般に,4階の等方テンソルは3つの自由度をもって次のように書けることが知られている.ただし,
は4階テンソルである.さらに,流体が等方的な物質であれば,これらは等方的なテンソルでなければならない.一般に,4階の等方テンソルは3つの自由度をもって次のように書けることが知られている.ただし,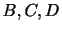 はスカラーである.
これを(2.33)に代入すれば,
はスカラーである.
これを(2.33)に代入すれば,
ただし,
とおき,また変形速度テンソルが対称テンソルである(
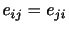 )であることを用いた.さらに,
)であることを用いた.さらに,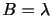 ,
,
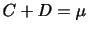 とおけば,
を得る.さらに,偏差応力テンソルの対角成分の和は0となるので,
であり,これより
でなければならない.したがって,偏差応力テンソルは
とおけば,
を得る.さらに,偏差応力テンソルの対角成分の和は0となるので,
であり,これより
でなければならない.したがって,偏差応力テンソルは
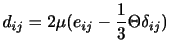 |
(3.35) |
と表される.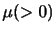 は粘性に関係する物質定数で,粘性率,粘性係数(coefficient of viscosity)と呼ばれる.右辺の
は粘性に関係する物質定数で,粘性率,粘性係数(coefficient of viscosity)と呼ばれる.右辺の
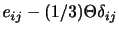 も対角和が0を満たしていることに注意が必要である.なお,(2.35)の形は(2.32)とも一致している.また,粘性率を物質の密度で割った値(
も対角和が0を満たしていることに注意が必要である.なお,(2.35)の形は(2.32)とも一致している.また,粘性率を物質の密度で割った値(
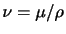 )は動粘性率(kinematic viscosity)と呼ばれる.
)は動粘性率(kinematic viscosity)と呼ばれる.
以上をまとめれば,ニュートン流体における応力テンソルは
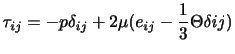 |
(3.36) |
となる.ただし,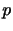 は(2.30)により定義される.特に非圧縮な流れ(
は(2.30)により定義される.特に非圧縮な流れ(
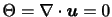 )では,
)では,
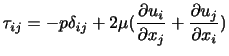 |
(3.37) |
である.
#.




: 2
: 運動している流体と応力テンソル
: 流体の局所的運動と変形
目次
Yuta
平成22年1月23日