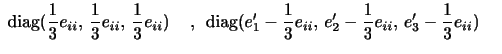: 変形速度と応力の関係
: 運動している流体と応力テンソル
: 運動している流体と応力テンソル
目次
ある流体要素の中心Pの位置ベクトルを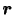 ,その流体要素の他の任意の点Qの位置ベクトルを
,その流体要素の他の任意の点Qの位置ベクトルを
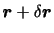 とする.このとき,相対速度
とする.このとき,相対速度
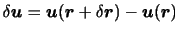 を調べることによって,変形の様子を知ることができる.
を調べることによって,変形の様子を知ることができる.
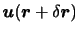 を
を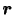 まわりでテイラー展開して,微少量
まわりでテイラー展開して,微少量
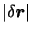 の2次以上の項を無視すると,
の2次以上の項を無視すると,
となる.
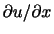 等の微分係数は点Pにおける値である.第1項の
等の微分係数は点Pにおける値である.第1項の
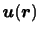 は,その流体要素の全体としての剛体的な並進運動を表す.残り9項の合成が点Qの点Pに対する相対運動を表す.
は,その流体要素の全体としての剛体的な並進運動を表す.残り9項の合成が点Qの点Pに対する相対運動を表す.
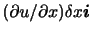 で表される運動は,
で表される運動は,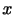 軸方向を向き,
軸方向を向き,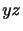 面からの距離
面からの距離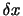 に比例するようなもの,すなわち,
に比例するようなもの,すなわち,
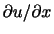 が正(負)ならば,
が正(負)ならば,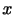 方向に一様な伸び(縮み)を表す(図2.7).同様に,
方向に一様な伸び(縮み)を表す(図2.7).同様に,
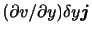 および
および
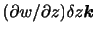 はそれぞれ
はそれぞれ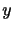 方向,
方向,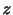 方向の一様な伸びあるいは縮みを表している.
方向の一様な伸びあるいは縮みを表している.
一方,
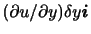 は
は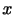 方向の運動であるが,その速度の大きさは
方向の運動であるが,その速度の大きさは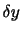 に比例する.これは図2.8のような
に比例する.これは図2.8のような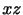 平面に平行な平面の
平面に平行な平面の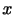 方向のずれ運動あるいはせん断運動を表す.残りの他の項についても同様である.
方向のずれ運動あるいはせん断運動を表す.残りの他の項についても同様である.
相対速度をテンソル表記で書けば,
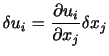 |
(3.24) |
となる.行列
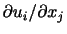 は2階テンソルであって,速度勾配テンソル(velocity gradient tensor)と呼ばれる.ここで,速度勾配テンソルを対称テンソルと反対称テンソルに分解することを考える.すなわち,
とすると,
は2階テンソルであって,速度勾配テンソル(velocity gradient tensor)と呼ばれる.ここで,速度勾配テンソルを対称テンソルと反対称テンソルに分解することを考える.すなわち,
とすると,
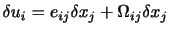 |
(3.25) |
となる.これにより,相対速度への寄与を対称テンソルによるものと反対称テンソルによるものとに分割することができる.
反対称テンソル
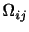 については,速度場
については,速度場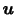 の回転(rotation)として知られているベクトル場
の回転(rotation)として知られているベクトル場
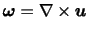 の成分
の成分
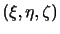 を用いることによって
を用いることによって
と表される. ベクトル
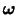 は渦度(vorticity)と呼ばれる.
は渦度(vorticity)と呼ばれる.
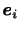 を(2.25)にかけて
を(2.25)にかけて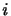 について加えれば,
について加えれば,
となるが,ここで
なので,
を得る.(2.26)の1行目は,座標軸方向の一様な伸び(あるいは縮み)に対応する.2行目の
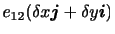 は,図2.7のような
は,図2.7のような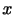 軸と
軸と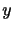 軸のなす角が単位時間当たり
軸のなす角が単位時間当たり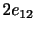 だけ減少する,正方形がひし形にひしゃげるような純粋なずれ運動に対応する.2行目の残りの項も同様である.一方,3行目は角速度(angular velocity)
だけ減少する,正方形がひし形にひしゃげるような純粋なずれ運動に対応する.2行目の残りの項も同様である.一方,3行目は角速度(angular velocity)
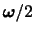 の剛体的回転(rigid body rotation)による速度場を表している.
の剛体的回転(rigid body rotation)による速度場を表している.
図 2.9:
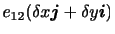 に対応する純粋な変形運動
に対応する純粋な変形運動
|
|
このように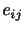 は流体要素の変形の速度(割合)を表すので,変形速度テンソルあるいはひずみ率テンソル(rate-of-strain tensor)と呼ばれる.このテンソルは対称テンソルであるので,座標軸を主軸座標系に変換すれば,
は流体要素の変形の速度(割合)を表すので,変形速度テンソルあるいはひずみ率テンソル(rate-of-strain tensor)と呼ばれる.このテンソルは対称テンソルであるので,座標軸を主軸座標系に変換すれば,
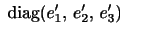 |
(3.27) |
の形に帰着できる.つまり,流体要素の変形は対称テンソルの主軸方向の一様な伸びまたは縮みのみによって表されることになる.また,対角成分の和
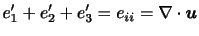 |
(3.28) |
は,後に述べるが流体要素の体積膨張率である.応力テンソルのときと同様に(2.27)を等方テンソルとそのずれに分解すると,
となる.前者は等方的な(2.28)に対応する膨張あるいは収縮であり,後者は体積変化を伴わない球を楕円体にひしゃげるような純粋な変形運動に対応する.
以上より微小な流体要素の運動は,次のような運動を同時に行っているといえる.
- 中心における流速
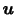 での全体としての剛体的並進運動.
での全体としての剛体的並進運動.
- 角速度
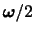 の剛体的回転(自転)
の剛体的回転(自転)
- 球を楕円体にひしゃげるような体積変化を伴わない純粋な変形運動
-
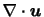 の割合での等方的な膨張(あるいは収縮)運動
の割合での等方的な膨張(あるいは収縮)運動
(2)は反対称テンソル
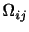 からくる.一方,変形運動(3),(4)は対称テンソル
からくる.一方,変形運動(3),(4)は対称テンソル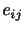 からくる.また,(1),(2)は剛体的運動であり,(3),(4)は変形体特有の運動である.密度一定の完全流体おける渦なし流れ(
からくる.また,(1),(2)は剛体的運動であり,(3),(4)は変形体特有の運動である.密度一定の完全流体おける渦なし流れ(
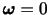 の流れ)では,
の流れ)では,
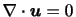 なので,流体要素は並進しながら純粋な変形運動(3)のみを行うことになる.
なので,流体要素は並進しながら純粋な変形運動(3)のみを行うことになる.




: 変形速度と応力の関係
: 運動している流体と応力テンソル
: 運動している流体と応力テンソル
目次
Yuta
平成22年1月23日
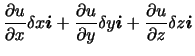
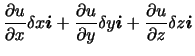
![]() は
は![]() 方向の運動であるが,その速度の大きさは
方向の運動であるが,その速度の大きさは![]() に比例する.これは図2.8のような
に比例する.これは図2.8のような![]() 平面に平行な平面の
平面に平行な平面の![]() 方向のずれ運動あるいはせん断運動を表す.残りの他の項についても同様である.
方向のずれ運動あるいはせん断運動を表す.残りの他の項についても同様である.
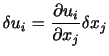
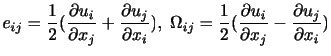
![]() については,速度場
については,速度場![]() の回転(rotation)として知られているベクトル場
の回転(rotation)として知られているベクトル場
![]() の成分
の成分
![]() を用いることによって
を用いることによって
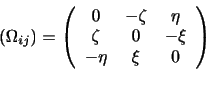
![]() を(2.25)にかけて
を(2.25)にかけて![]() について加えれば,
について加えれば,