



: 運動方程式
: 質量保存則
: 質量保存則
目次
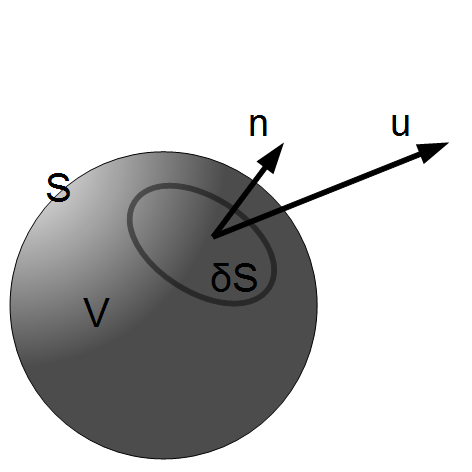
ここで,図3.1のような空間に固定した閉じた曲面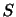 を考える.
を考える.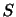 で囲まれた領域を
で囲まれた領域を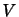 とする.
とする.
図 3.1:
空間に固定された閉じた領域
l6.5cm
|
任意の時刻において,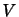 内の流体の質量は
である.したがって,
内の流体の質量は
である.したがって,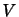 内の流体の単位時間当たりの質量の増加は
で与えられる.一方,
内の流体の単位時間当たりの質量の増加は
で与えられる.一方,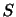 を通って単位時間当たりに
を通って単位時間当たりに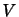 から流出する流体の質量は,微小な面要素
から流出する流体の質量は,微小な面要素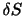 を通って単位時間当たりに流出する質量
を通って単位時間当たりに流出する質量
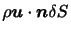 を
を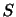 全体で加え合わせれば
である.ただし,
全体で加え合わせれば
である.ただし,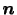 は
は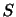 の外向き単位法線ベクトルである.流体が新たに発生あるいは消滅したりしない限り,
の外向き単位法線ベクトルである.流体が新たに発生あるいは消滅したりしない限り,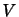 内の流体の質量増加は境界面
内の流体の質量増加は境界面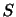 を通って流体質量が流入したことによるので,次式が成り立つ.
ここで,ガウスの定理を用いて右辺の面積積分を体積積分に変換して,移行すれば
を通って流体質量が流入したことによるので,次式が成り立つ.
ここで,ガウスの定理を用いて右辺の面積積分を体積積分に変換して,移行すれば
を得る.上式が任意の領域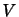 に対して常に成り立つためには
に対して常に成り立つためには
 |
(6.41) |
が成り立つ必要がある.この式が質量保存則のひとつの表現であり,連続の式(equation of continuity)と呼ばれる.また,ベクトル公式
を用いれば,連続の式(3.4)は次のように書き換えることもできる.
 |
(6.42) |
流体粒子の密度が運動中変わらないとき,すなわち
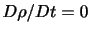 であるとき,流れは非圧縮(incompressible)であるという.このとき連続の式は
であるとき,流れは非圧縮(incompressible)であるという.このとき連続の式は
 |
(6.43) |
に帰着する.
Yuta
平成22年1月23日
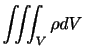
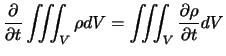
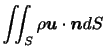
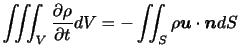
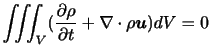
![]() であるとき,流れは非圧縮(incompressible)であるという.このとき連続の式は
であるとき,流れは非圧縮(incompressible)であるという.このとき連続の式は